哈夫曼树与编码
哈夫曼树定义:
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman
Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
例:在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。例如,需传送的报文为“AFTER DATA EAR ARE ART AREA”,这里用到的字符集为“A,E,R,T,F,D”,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。要区别6个字母,最简单的二进制编码方式是等长编码,固定采用3位二进制,可分别用000、001、010、011、100、101对“A,E,R,T,F,D”进行编码发送,当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。
哈夫曼树创建方法
2.1 初始队列
我们按出现频率高低将其放入一个优先级队列中,从左到右依次为频率逐渐增加。

下面我们需要将这个队列转换成哈夫曼二叉树,哈夫曼二叉树是一颗带权重的二叉树,权重是由队列中每个字符出现的次数所决定的。并且哈夫曼二叉树始终保证权重越大的字符出现在越高的地方。
2.2 第一步合并
首先我们从左到右进行合并,依次构建二叉树。第一步取前两个字符u和r来构造初始二叉树,第一个字符作为左节点,第二个元素作为右节点,然后两个元素相加作为新空元素,并且两者权重相加作为新元素的权重。
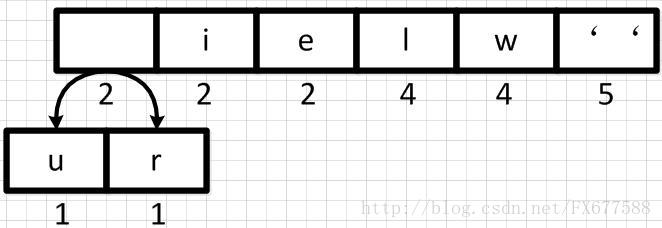
同理,新元素可以和字符i再合并,如下:
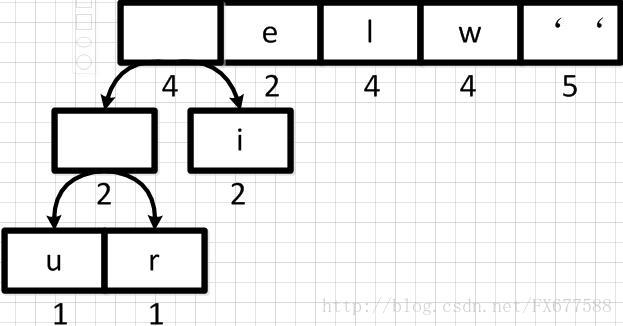
2.3 重新调整队列
上图新元素权重相加后结果是变大了,需要对权重进行重新排序。
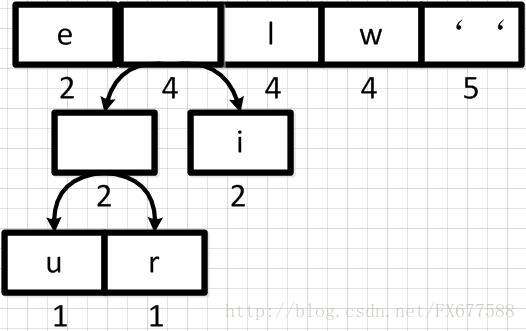
然后再依次从左到右合并,每合并一次则进行一次队列重新排序调整。如下:
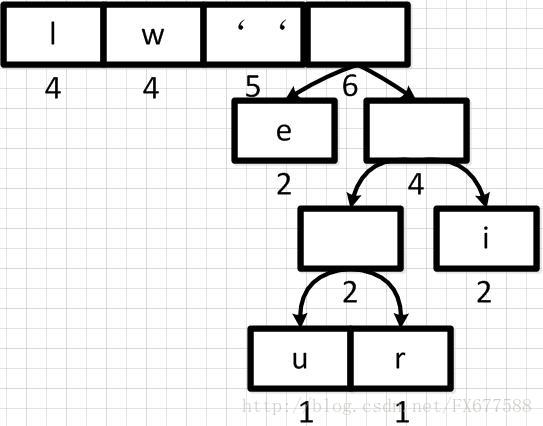
经过多步操作之后,得到以下的哈夫曼二叉树结构,也就是一个带有权重的二叉树:
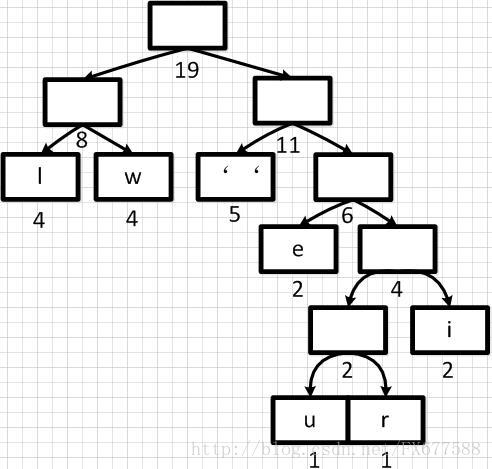
2.4 哈夫曼编码
有了上面带权重的二叉树之后,我们就可以进行编码了。我们把二叉树分支中左边的支路编码为0,右边分支表示为1,如下图:
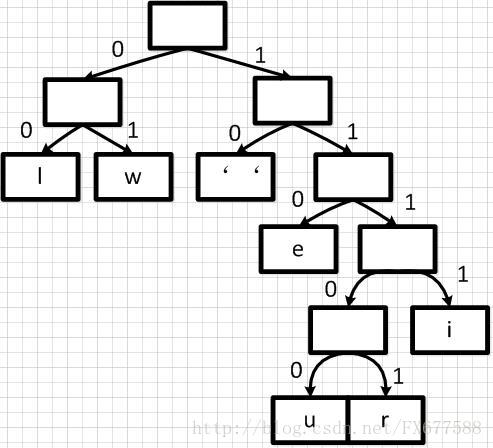
这样依次遍历这颗二叉树就可以获取得到所有字符的编码了。例如:‘ ’的编码为10,‘l’的编码为00,‘u’的编码为11100等等。经过这个编码设置之后我们可以发现,出现频率越高的字符越会在上层,这样它的编码越短;出现频率越低的字符越会在下层,编码越短。经过这样的设计,最终整个文本存储空间才会最大化的缩减。
最终我们可以得到下面这张编码表:

2.5 字符串编码
有了上面的编码表之后,”we will we will r u”这句重新进行编码就可以得到很大的压缩,编码表示为:01 110 10 01 1111 00 00 10 01 110 10 01 1111 00 00 10 11101 10 11100。这样最终我们只需50位内存,比原ASCII码表示节约了2/3空间,效果还是很理想的。当然现实中不是简单这样表示的,还需要考虑很多问题。
三、哈夫曼编码的压缩与解压
1、使用IO流逐字节读取文档。用一个数组(0~255,下标表示ASCII码)来保存不同字符出现的次数
2、建一个节点类,保存节点对象的信息。将数组每一位表示的字符和出现频次存入创建的节点,把所有节点存入一个链表。
3、根据节点存储的频次值,对链表进行从小到大排序
4、从链表中取出并删除最小的两个节点,创建一个他们的父节点,父节点不存字符,值为那两个节点的和,把那两个节点分别作为其左子节点和右子节点,最后把这个父节点存入链表。再次排序,取出并删除最小的两个节点,生成父节点,再存入…以此类推,最终生成一棵哈夫曼树。
5、对哈夫曼树进行遍历,使得叶子结点获得相应编码,同时把字符和它对应的哈夫曼编码存入HashMap
四、疑问
4.1对于字符频率相等的情况
我们在构建哈夫曼树的时候在想,如果我们的字符出现的频率相等的情况,那哈夫曼树岂不是很糟?
我们假设原来字符串长度为N,那么对于普通的ASCII编码得到的长度为8N,如果利用哈夫曼编码,对于每一个字符,最大的长度不会超过8层树因为ASCII编码总共只有2^8个字符,也就是说最极端的情况:一个文件中所有字符串中出现256个字符且重复次数是一样的,但这仍然对原来的文本有进行过压缩(毕竟出现次数相等的话,构造的哈夫曼树在8层之前还是有数据的,那些数据的位数<8)最终的编码数一定是会<8N
4.2解码冲突问题
我们在解压遍历哈夫曼的时候,最终的编码不会冲突么?举例:上面我们得到得最终的编码是
01 110 10 01 1111 00 00 10 01 110 10 01 1111 00 00 10 11101 10 11100但是在实际的压缩中我们不会有分隔符最终的情况将会是:
0111010 0111110000100111010011111000010111011011100
于是我们怎么知道:前面的01是一个编码,为什那么0111就是一个编码呢?也就是说01是0111的前缀 。其实我们从这张图就能看出来:对于上述的字符串一定不会存在一个叫0111的编码,因为“w”字母代表的01已经没有子节点。其实中也可以看出一些区域是空着的比如:11、111、111、1110 没有数据,其实这都是满足了哈夫曼树的 左起字串不冲突原则
